International Journal of Environmental Pollution and Remediation (IJEPR)

ISSN: 1929-2732

1. Introduction

The present paper investigates uranium mobility in a rendosol developed on a cretaceous chalk formation. Uranium deposits from specific activities on the soil surface continuously exposed to weathering, lead to oxidation of U(0) into solid mixed U(IV)/U(VI) oxides (Haschke, 1998; Salbu et al., 2003). Leaching of fragmented uranium oxide by rainfall then produces highly soluble U(VI) compounds (McEachern and Taylor, 1998). Uranium is known to interact strongly with both organic and mineral components of soils: his potential mobility is thus highly limited in oxic and suboxic conditions (Ragnarsdottir and Charlet, 2000). The behaviour of uranium in subsurface environments is strongly related to matrix composition and baseline geochemistry, which is driven by water-rock interactions.

The main geochemical mechanisms are relatively well-known in chalk aquifers (Edmunds et al., 2003). They are primarily controlled by the infiltration of diluted water enriched in carbon dioxide and calcite equilibrium under open conditions in the vadose zone, where pC0₂ is kept constant (infinite reservoir), and close conditions in the saturated zone where pC0₂ is controlled by water-rock interactions (Appelo, 2005). Since the kinetics of calcite dissolution are fast, a relative homogeneity of the aquifer baseline chemistry is reached in terms of pH, alkalinity and Ca concentration.

Based on a wide set of data measured in an array of wells, boreholes and trenches, this modelling study aims at developing a vertical one-dimensional (1D) reactive transport model for uranium migration through soil toward unconfined chalk aquifer, by considering unsaturated zone (in a simplified manner) and top of the saturated zone, both in a dual porosity pattern including the chalk matrix and the interconnected fracture network. This work illustrates an integrated approach from the field to numerical modelling that allows diagnosis of soil pollution and further evaluation of radionuclide migration in subsurface environment, giving keys for enhancing treatment and remediation of polluted soils.

2. Field Works

2. 1. Sampling and Analytical Methods

Distribution of uranium in surface soils was determined by soil sampling followed by gamma-ray spectrometry using Ge crystals, considering the 63 keV line of ²³⁴Th and assuming a secular equilibrium between ²³⁸U and ²³⁴Th. One meter deep vertical trenches, as well as deep drills, were dug close to deposit in order to evaluate both soil composition and the uranium migration pattern with depth. Soil was sampled in the 0-15 cm deep layer and was sieved to 2.0 mm diameter. Major and trace elements have been analysed in both bulk soils and rock samples by X-fluorescence spectrometry and ICP-mass spectrometry after complete digestion by alkaline melting. The mineral phases have been determined by X-ray diffraction (XRD), with specific determination of mixed-layer minerals and expandable phyllosilicates in the < 2 μm clay fraction after orientation and exposure to ethylene-glycol.

The groundwater samples were collected in piezometers by pumping after purge of the water column, and in two springs using Nalgène™ bottles (Nalge Nunc International Corporation, Rochester, New-York, USA). Eh, pH, temperature and specific conductivity have been measured on-site in boreholes using combined YSI 600 XLM multi-parameter probes (YSI, USA). Some wells were designed for groundwater quality monitoring and determination of baseline geochemistry. Interstitial water from unsaturated zone rock samples were extracted by core centrifugation. Major elements were analysed by ionic chromatography and trace elements (including uranium) by ICP-mass spectrometry after on-site sample filtration through 0.45 μm cellulose filters and acidification with ultrapure 60% HNO3 (Merck KGaA, Darmstadt, Germany).

2.2. Hydrogeochemical Background

The composition of geological materials (soils and rocks) and groundwater baseline are determined in reference area located close outside the contaminated zone, in similar geological units. The calcium carbonate content in the chalk is generally above 95% whereas it ranges between 60 and 80% in colluviums and soils (Table 1). The non-carbonate fraction is composed by silicates (opal-CT, quartz, micas and feldspars), clay minerals (mainly kaolinite, illite and chlorite,) and Al-Fe oxide or hydroxide mixtures. Soils and colluviums are characterised by a larger non-carbonate fraction than in the Chalk units. Uranium content of unpolluted soils, colluviums, cryoturbated and chalk are typically lower than 1.5 mg.kg^-1. The chalk is characterized by a total porosity of 40%, including about 1% vol. related to the fracture network. Meteoric precipitations constitute the only aquifer recharge. The hydraulic conductivity of the matrix ranges between 10^-9 and 10^-7 m.s^-1, and the overall hydraulic conductivity of the bulk chalk can reach 10^-6 m.s^-1 due to the presence of fractures (Bourdon et al., 2009).

Table 1. Mineralogical composition, specific surface area and kinetic parameters used in reactive transport models. Chalk is simulated by a composite carbonate solid solution containing Ca, Sr, Mg and traces of U, with stoechiometries as given below. Adapted from Gillon et al., 2010.

	Content [kg.L-1]	Specific surface(1) [m2.g-1]	Kinetic rate [mol.m-2.s-1]
Chalk (Calcite with Sr, Mg  and U impurities)*	7.86	0.02	-12.1
Cristobalite-a SiO2 (surrogate of opal-CT)	0.02	0.02	-11.3
K-Feldspar KAlSiO3	0.02	0.02	-12
Kaolinite Al4(Si4O10)(OH)8	0.06	10	-14
Goethite (in soil and surface soil) FeOOH	0.8	35	-7.95
Goethite (in chalk)	0.08	35	-7.95
Uraninite (in surface soil) UO2	0.005	0.001	-10.1

*Chalk composition, stoichiometry and kinetics are taken from Gillon et al. (2010), and brought back to 1 mole of CO₃^2-:

Chalk composition:	Ca0.9937Mg0.005Sr0.0013U0.00000005(CO3)
Chalk + H+→ 0.9937 Ca2+ + 0.005 Mg2+ + 0.0013 Sr2+ + 0.00000005 UO22+ + HCO3– , log K ~ log Kcalcite =1.84 at 25°C

The unsaturated zone in the studied area has been measured up to a depth ranging from 25 to 45 m beneath the surface. The mean annual infiltration rate is estimated to be around 150 mm.yr^-1, and the mean annual groundwater temperature is 12 °C. Baseline groundwater composition is driven by water-rock interactions, and determined from statistical analysis in an array of reference wells representative of groundwater streaming in unconfined chalk aquifer at the watershed scale, over five years of monitoring (Table 2). The composition of the bulk groundwater is roughly homogeneous and consistent with a calcium-bicarbonate-rich reservoir representative of the chalk aquifer: all groundwaters are at (or close to) saturation with calcite. The Ca²⁺ and HCO₃– concentrations corresponding to the equilibrium between water and calcite are rapidly reached, and hardly evolve towards water table due to the congruent dissolution of carbonate minerals in the unsaturated zone.

Thus the spatial heterogeneity of rock composition in the geological substratum is not likely to have a major effect in the aqueous chemistry of the system (Gillon et al., 2010). Typical concentrations for natural uranium in the geochemical background are very low and range from 0.2 to 0.8 μg.L^-1.

Table 2. Mean, minima, maxima and other statistical parameters of chemical concentrations and physical parameters in groundwater baseline, with comparison to modelling results detailed in section 3.1.

	Unit	Mean	Median	Standard deviation	Minimum	Maximum	Modelling results (stationnary)
T	°C	11.7	11.7	1.3	6.7	16.6	12.0
pH	-	7.2	7.3	0.3	6.5	8.0	7.03
Conductivity	µS.cm–1	466	448	147	64	919	-
Eh	mV	437	423	61	315	668	470
Alkalinity	meq.L–1	4.2	3.8	1.4	2.2	8.4	4.08
HCO3–	mg.L–1	231.8	225.7	73.2	91.5	506.3	449
Ca2+	mg.L–1	88.1	88.1	32.0	16.0	264.5	115
Mg2+	mg.L–1	0.72	0.63	0.48	0.14	4.7	0.74
Sr2+	mg.L–1	0.35	0.35	0.17	0.087	1.05	0.69
Na+	mg.L–1	3.8	3.19	2.0	1.79	12.09	-
K+	mg.L–1	0.93	0.70	0.74	0.23	3.2	4.39
Cl–	mg.L–1	9.5	5.4	8.8	1.80	47.6	-
NO3–	mg.L–1	13.5	9.4	11.9	0.062	45.0	6.9
SO42–	mg.L–1	6.5	4.3	4.7	0.67	18.0	-
F–	mg.L–1	0.32	0.27	0.22	0.085	1.37	-
SiO2(aq)	mg.L–1	4.0	3.9	0.90	1.26	7.6	12.9
U(aq)	µg.L–1	0.46	0.45	0.13	0.24	0.77	0.05
S.Icalcite	/	-0.1	0.0	0.2	-0.5	0.4	0.0
S.Idolomite	/	-2.1	-2.1	0.5	-2.8	-1.1	-2.33

2.3. Uranium Distribution in Subsurface and Groundwater

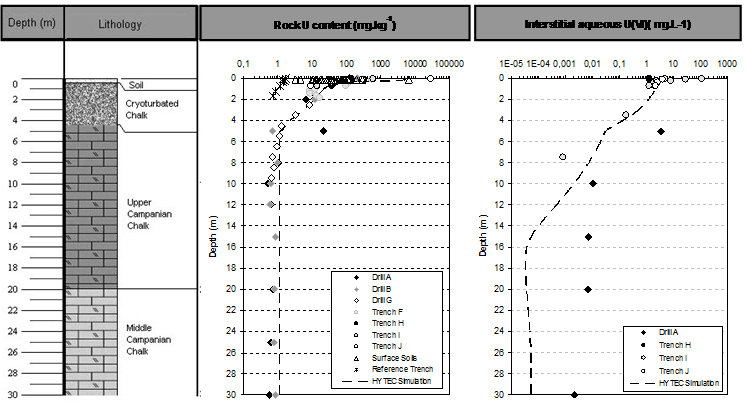
The extent of the subsurface anthropogenic uranium deposit is spatially limited, and lays in the top 20 cm of soil. Typical uranium concentration in surface soil ranges from < 1 g.m^-2 in uncontaminated areas, up to 50 g.m^-2 in contaminated soil. Around deposit, a characteristic yellow dusty cortex, produced by the oxidative dissolution of U(IV) dioxide, is made of crystallized uranyl hydroxides, mostly schoepite (UO₃.2H₂O), as shown by X-Ray diffraction. Infiltration of rainwater through soil ensures the migration of soluble uranium species towards the water table. The vertical extent of uranium migration downwards soil surface is at most 5 m (Fig. 1). Subsurface uranium content decreases sharply by more than five orders of magnitude.

The vertical migration of uranium in soil is thus mainly limited to the immediate surrounding of the polluted soils, and does not extend deeper than cryoturbated chalk level. Deeper in bulk chalk, uranium concentrations are consistent with those of the geochemical background, as found in the reference drill. The migration of uranium towards deeper horizons is thus strongly limited by retention onto solids surfaces.

Typical concentrations for aqueous uranium in groundwater underneath deposits vary from 1 to 10 μg.L-1 (Table 3). Seasonal variations of uranium concentration in groundwater do not exceed one order of magnitude and are not significant. Downstream the area of polluted soils, aqueous uranium concentration in groundwater decreases gradually towards geochemical baseline, so the longitudinal extend of the uranium plume along a flow line does not exceeds 500 m.

Table 3. Global statistics on aqueous uranium concentration in groundwater in wells.

Well #	Mean	Median	Standard deviation	Minimum	Maximum
	U(aq)  µg.L-1
A	1.3	1.7	1.1	0.1	2.2
B	4.7	3.9	2.7	1.6	8.8
C	4.5	4.7	2.6	0.2	9.4
D	1.0	0.9	0.3	0.4	1.6
E	0.8	0.9	0.1	0.5	1.0

3. Geochemical and Reactive Transport Modelling

Essential quantities for the understanding of the behaviour of uranium in natural environments are the mobile and immobile fractions of the uranium phases. For this study, we used the geochemical code CHESS, developed to solve a set of non-linear, multi-dimensional equations resulting from a mathematical description of a chemical system (van der Lee and De Windt, 2002). Aqueous and surface complexation onto mineral, colloidal or organic phases is accounted for, with or without the electrostatic effect on the surface reaction. An important aspect of the thermodynamic approach is the use of formation constants, hence the need for extended databases. The CHESS default database used in this study is based on a moderated version of the LLNL's EQ3/6 (Wolery, 1992), but extended to surface sites and colloidal species, and slightly modified to account for recent thermodynamic data for uranium (Guillaumont et al., 2003; Stewart et al., 2010) and carbonates phases (Hummel et al., 2002).

Reactive transport modelling of uranium was performed by using the code HYTEC (van der Lee et al., 2003). HYTEC simulates advective, dispersive and diffusive transport for solutes. The code is based on a finite element discretization in a representative elementary volume approach, and integrates CHESS for calculation of chemical equilibriums during transport.

Dual porosity in a fractured porous medium is formally represented by square block-matrix of definite length, where diffusion only occurs, and an implicit network of interconnected fractures subjected to an average advective flow. The competition between relative velocities of groundwater flow and chemical processes requires modelling using kinetic rate formulations. Main chemical, kinetic and hydrogeological parameters used in the following modelling are shown respectively in Table 3 and Table 4.

The chalk geochemistry has been determined using a solid solution approach for the modelling of calcite dissolution, on the basis of chalk bulk geochemistry and mineralogy (Table 1), as determined from samples taken from boreholes (Gillon et al., 2010).

Modelling of subsurface geological formations is conducted using three different layers, with respect to lithology and FeOOH content given in Fig. 1:

1- Surface soil layer: 0-0.25 m, goethite-enriched (0.8 kg.L^-1) and containing 5 g.L^-1 of uraninite as anthropogenic uranium pollution source,

2- Cryoturbated chalk: 0.25-5 m, goethite-enriched (0.8 kg.L^-1),

3- Chalk: 5 -30 m, low goethite content (0.08 kg.L^-1),

Table 4. Hydrogeological parameters considered in the reactive transport modelling.

	Chalk matrix	Fracture network
Porosity w [%]	37.5	2.5
Water saturation [%]	50 100	50 100
Hydraulic conduct. K [m.s-1]	-	1×10-6
Dispersivity a [m]	0.1	0.1
Pore diffusion coeff. Dp [m2.s-1]	10-10	10-9
Effective infiltration rate [mm.yr-1]	150
Depth of water table [m]	30
Block-matrix size (fractures spacing) L [m]	0.1

Vertical one-dimensional (1D) calculations were performed from topsoil to water table, with regards to the lithology met in the first 30 meters of subsurface formations, according to Fig. 1. Sorption of U(VI) onto goethite surface is simulated in a simple manner considering a non-electrostatic surface complexation model and a single sorption site, defined by an exchange capacity of 3.6 μmol.m^-2, and a formation constant log K(Goeth≡UO₂OH) = -3.7 (Zhijun et al., 2009).

3. 1. Geochemical Background

Calculations were performed to reproduce the field observations for CO₂ partial pressures close to 0.1 atm in soil. Since the carbonate dissolution in unsaturated zone is rapid and fully controlled by the CO₂ partial pressure in an open system (infinite CO₂ reservoir) (Langmuir, 1997), available CO₂ is kept constant during the calculation. Redox potential measurements fluctuated around + 450 mV, which is highly related with the dominance of nitrate reduction processes in the vadose zone (Appelo, 2005). In the unsaturated zone, the fast mineralisation of infiltrated rainwater due to congruent dissolution of chalk is responsible for the interstitial water composition to be representative of the stoichiometry of the composite carbonate phase (Table 1). Below water table, close conditions with respect to atmospheric conditions were assumed, so pCO₂ is left free to float: variation of groundwater composition along the flow path is thus mainly time dependent, as a consequence of slow water-rock interactions, especially the incongruent dissolution of chalk with reprecipitation of secondary pure calcite (Edmunds et al., 2003). This latter process has already been described in literature at the catchment's scale but can be neglected in this study due to the smaller scale of modelling. Calculated mean stationary groundwater composition after many decades of flow simulation into the unsaturated zone is given in Table 2. Modelling results are in good agreement with baseline geochemistry characterized from field observations. Aqueous uranium concentration in baseline groundwater, due to steady-state chalk congruent dissolution, is calculated close to 0.05 μg.L^-1, in the lower range of corresponding field observations.

3. 2. Uranium Migration

Anthropogenic uranium deposits are integrated into the global scheme of water-rock interactions forming the geochemical background framework in chalk describe above a 25 cm layer of uraninite-enriched soil is set at the soil surface.

Uraninite dissolution is kinetically controlled, using apparent dissolution rate 3 orders of magnitude lower than ones measured on comparable materials under laboratory conditions (Handley-Sidhu et al., 2009). Vertical distribution of fixed uranium in subsurface materials is given in Fig. 1: simulated profile is found to be in close agreement with measurements conducted on soil and rock samples. Predicted uranium concentrations in both the solid phase and the aqueous phase (e.g. interstitial water in the unsaturated zone) are close to observed ones, both in the uranium migration front (in the upper part of the profile), and in the geochemical background (in the lower part of the profile). Compared evolution with time of aqueous concentration of uranium in chalk groundwater are given in Fig. 3, from both field observations following more than 10 years of water quality monitoring, and predicted by numerical modelling.

During a first period of about 70 years, no breakthrough of anthropogenic uranium is predicted by numerical modelling: reactive transfer of uranium through the unsaturated zone is not achieved, and aqueous concentration found in groundwater is set by release of natural uranium impurities following congruent dissolution of chalk.

After more than 80 years of flow modelling, a possible delayed breakthrough of anthropogenic uranium is predicted, as a result of reactive transport of U(VI) driven by strong adsorption on goethite onto subsurface materials. Numerical predictions are not totally in agreement with field observations from groundwater monitoring:

• As shown above, uranium concentrations in geochemical baseline is in fair agreement with field data,
• An anticipated breakthrough of anthropogenic uranium is observed from field monitoring in wells located closely downstream of polluted soils.
• This breakthrough cannot be explained considering a transport model only controlled byn retardation of uranium migration induced by adsorption onto mineral phases.

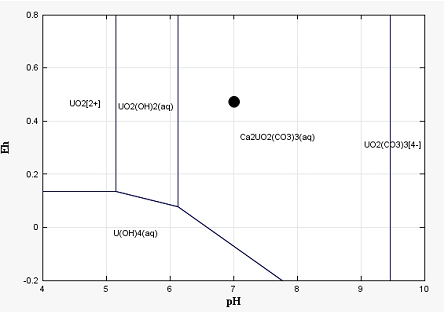
As shown by uranium profiles in the solid phase, aqueous speciation of U(VI), mainly found to be controlled by mobile Ca-U(VI)-Carbonates complexes, does not inhibit uranium sorption on goethite. Thus, aqueous uranium concentrations observed in groundwater closely downstream polluted soils may be induced either by colloidal transport (Claveranne-Lamolère et al., 2009) or kinetically-controlled adsorption and release of uranium by mineral phases (Braithwaite et al., 1997; Gabriel et al., 1998), or by an additional but fast migration in fractures network (Brouyère, 2006). Such processes, out of the range of the present paper, will be considered in future developments.

4. Conclusions

Reactive transport models offer the mean of studying geochemically complex systems in a hydrodynamic context, at the field scale. A growing number of processes, among dissolution/precipitation mechanisms, reversible adsorption and redox equilibrium, both at thermodynamic equilibrium or under kinetic control, can be taken into account simultaneously for a better representation of reality.

In this study, numerical modelling applied to uranium behaviour in natural subsurface environment shows that main geochemical processes describing uranium retention and migration in subsurface can be reasonably described and predicted, throught additional processes such as colloidal migration or fast migration in fracture still remained to be assessed. At larger scales, including both vadose zone and groundwater, increasing complexity of the models needs a deep conceptual and quantitative understanding of such natural environments, with a careful fit to field data.

References